Wiek XVI, który dał początek współczesnemu rozwojowi nauki, zaznaczył się silnym rozwojem algebry. Między innymi zostały w tym czasie podane wzory wyrażające pierwiastki równań stopni 3 i 4 przez współczynniki tych równań za pomocą pierwiastków drugiego i trzeciego stopnia.
Wówczas pojawiło się zjawisko paradoksalne:
Rozwiązać można tymi wzorami równanie stopnia trzeciego, które ma trzy różne pierwiastki rzeczywiste, tylko wtedy, gdy umie się obliczyć 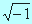 . Oczywiście w zakresie liczb do tego okresu znanych pierwiastek kwadratowy z -1 nie istniał. Nie kłopocząc się tym zbytnio, niektórzy z matematyków założyli jego istnienie i nazwali go liczbą urojoną, a poprzednio znane liczby nazwali rzeczywistymi.
. Oczywiście w zakresie liczb do tego okresu znanych pierwiastek kwadratowy z -1 nie istniał. Nie kłopocząc się tym zbytnio, niektórzy z matematyków założyli jego istnienie i nazwali go liczbą urojoną, a poprzednio znane liczby nazwali rzeczywistymi.
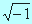 . Oczywiście w zakresie liczb do tego okresu znanych pierwiastek kwadratowy z -1 nie istniał. Nie kłopocząc się tym zbytnio, niektórzy z matematyków założyli jego istnienie i nazwali go liczbą urojoną, a poprzednio znane liczby nazwali rzeczywistymi.
. Oczywiście w zakresie liczb do tego okresu znanych pierwiastek kwadratowy z -1 nie istniał. Nie kłopocząc się tym zbytnio, niektórzy z matematyków założyli jego istnienie i nazwali go liczbą urojoną, a poprzednio znane liczby nazwali rzeczywistymi.
Wprowadzenie tych liczb w wieku XVI nie miało żadnego uzasadnienia logicznego, ani oparcia o bezpośrednią intuicję kierowaną przez zjawiska przyrodnicze. Wskutek tego powstały kontrowersje między matematykami, z których jedni używali tych liczb bez skrępowania, inni zaś zaprzeczali ich istnieniu.
Zwolennicy istnienia tych liczb działali nimi tak jak liczbami rzeczywistymi, dodając, odejmując, mnożąc i dzieląc. Oznaczali 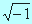 przez i przyjmując , że
przez i przyjmując , że 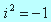 .
.
Swobodnie dodając i mnożąc liczby rzeczywiste i "urojone" tworzyli nowe "liczby" a+bi, które dziś nazywamy liczbami zespolonymi!!!
Arytmetyka tych liczb nie doprowadziła do sprzeczności. W 1748 roku Euler wprowadził je do analizy w swym fundamentalnym dziele "Introductio in analysin infinitorum", nie tylko nie dochodząc do sprzeczności, lecz powodując tym istotny postęp analizy.
Wkrótce stało się jasne, że liczby zespolone - mimo że brak im uzasadnienia logicznego - są jednym z najważniejszych narzędzi matematycznych dla badań zjawisk przyrodniczych, wskutek czego używanie ich jest w tej samej mierze słuszne, co używanie liczb rzeczywistych.
Początek wieku XIX zdarł wszelką mistykę z tych liczb, gdyż przyniósł ściśle ich uzasadnienie:
I Pierwsze z nich - Gaussa - wykazało, że liczby zespolone są to właściwie punkty płaszczyzny euklidesowej, w której wprowadzono pewne działania zwane dodawaniem i mnożeniem punktów czyli liczb zespolonych.
II Drugie uzasadnienie - Hamiltona - wprowadza liczby zespolone jako pary liczb rzeczywistych, z tym że określa się specjalny sposób mnożenia i dodawania par.
Z całej mistyki pozostała używana jeszcze do dziś nazwa liczby urojone, lecz w istocie rzeczy, są one równie rzeczywiste jak liczby rzeczywiste.

